Fractions Calculator - Fraction Multiplier, Addition, Subtraction, Division
Fraction Calculator
What is a Fraction? Parts and Meaning
A fraction, in the simplest meaning of the word, refers to a quantity that is not a whole, thus expressing a part-whole relationship. In terms of mathematics, a fraction represents a number of parts of a whole. So, if we represent 7 parts of a whole that has a total of 10 parts, then a fraction would be represented as 7 ÷ 10.
A fraction is represented in terms of the part and whole, separated by a line of division. A mathematical fraction also has 2 parts:
- Numerator: this appears on the top of the line of division and represents the part.
- Denominator: this appears below the line of division and represents the whole of which the numerator is a part.
For example, in the fraction 2 ÷ 7, 2 is the numerator and 7 is the denominator.
Types of Fractions
In mathematics, fractions can be of 6 major types, in which the categories are non-exclusive (i.e. a particular fraction can fall into more than one category).
- Proper Fraction
A proper fraction refers to a fraction which has a numerator that is smaller than the denominator. So, 8 ÷ 17, 2 ÷ 5, 1 ÷ 5 etc. are all examples of proper fractions as their numerators, i.e. the numbers above the division line (8, 2, 1) are smaller than the denominators, i.e. the number expressed below the division line (17, 5, 5).
- Improper Fraction
An improper fraction refers to a fraction in which the denominator is smaller than the numerator (conversely the numerator is larger than the denominator). So for instance, examples of improper fractions include 8 ÷ 5, 4 ÷ 3, 3 ÷ 2 .
- Like Fraction
Like fractions involve a pair of fractions which have the same denominator. Operations like addition and subtraction can be performed directly on like fractions. So for example, 49 and 79 are like fractions. Similarly, 3 ÷ 5 and 2 ÷ 5 are also like fractions
- Unlike Fraction
Unlike fractions refer to a pair of fractions in which the denominators are different. To perform operations like addition and subtraction on improper fractions, they must first be converted into like fractions. For example, 4 ÷ 9 and 5 ÷ 8 are a pair of unlike fractions since their denominators (9 and 8) are different and unequal.
In many mathematical operations, you may need to convert an improper fraction to proper fraction. Here is how you can do it:
Firstly, find the Lowest Common Multiple (LCM) of the fractions. For example, for 4 ÷ 6 and 5 ÷ 8 , the denominators are 6 and 8 and the LCM of 6 and 8 is 24.
After you have found the LCM of the denominators, the next step is to see which number you will have to multiply the denominators with to obtain the LCM. (An easy trick is to divide the LCM with the denominator). For example, in case of 8, it must be multiplied with 3 to obtain 24, and for 6, it must be multiplied by 4 to obtain 24
After finding out the factor by which the denominator has to be multiplied, multiply both the numerator and the denominator by the same number, i.e. 4 x 4 ÷ 6 x 4 = 16 ÷ 24 and 5 x 3 ÷ 8 x 3 = 15 ÷ 24
Now you have your like fractions, i.e. 16 ÷ 24 and 15 ÷ 24
- Mixed Fraction
A mixed fraction, as the name suggests, consists of a whole, and a part and its combined whole. It has two parts: a whole number and a fraction. A mixed fraction is obtained from an improper fraction when it is divided. The quotient obtained after the division forms the whole number, the remainder forms the numerator of the remaining fraction and the divisor forms the denominator.
Here is an example:
If we consider the improper fraction 85 and divide the numerator by the denominator through long division, we have:Divisor = 5
Quotient = 1
Remainder = 3
To convert this into a mixed fraction, the quotient becomes the whole, the remainder becomes the numerator and the divisor becomes the denominator, i.e 1 x 3 ÷ 5 .
- Equivalent Fraction
Equivalent fractions are those fractions that have the same reduced form, i.e. when reduced to their simplest forms, these fractions are equivalent. For example, upon reducing the two fractions 3 ÷ 6 and 2 ÷ 4 to their simplest form they will be 1 ÷ 2 and hence will form a pair of equivalent fractions.
Similarly the pair of fractions 9 ÷ 9 and 4 ÷ 4 will be equal to 1 ÷ 1 upon reduction to the simplest form which means they form a pair of equivalent fractions.
How to Perform Operations on Fractions
Performing mathematical operations on fractions may seem confusing or complex but if you remember certain thumb rules to approaching operations on fractions you can easily perform them. Here we have broken down the process of solving mathematical operations on fractions for you in simple steps.
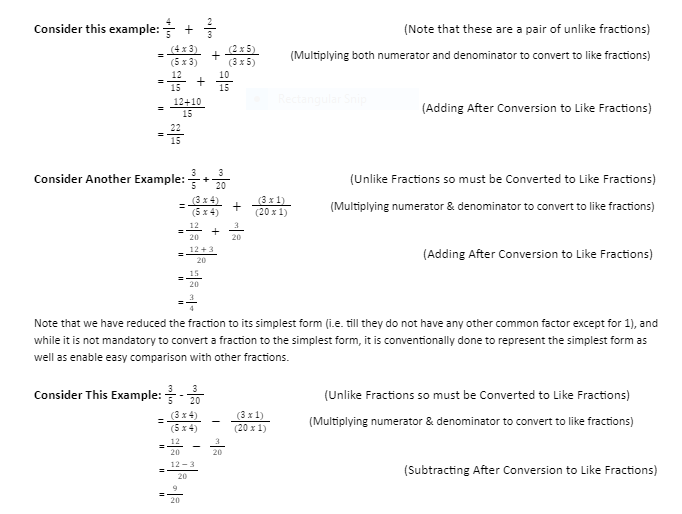
- Addition & Subtraction
The very first and foremost factor to keep in mind here is that whenever you are performing an addition or subtraction to a pair of fractions, they must be like fractions. Hence if the pair of fractions you are adding/subtracting is a pair of like fractions then you can directly add or subtract them. But in case they are unlike fractions, you should first convert them into like fractions as taught above.
- Multiplication and Division
For operations like multiplication and division, you can directly perform the calculations on the unlike pair of fractions.
Multiplication of fractions is really simple: first, you need to multiply the numerical values of the numerators and the denominators. Then simply the obtained answer to the reduced form.
Common Engineering Fraction to Decimal Conversions
In engineering, fractions are widely used to describe the size of components such as pipes and bolts. The most common fractional and decimal equivalents are listed below. (Need to change description)
| 64th | 32th | 16th | 8th | 4th | 2nd | Decimal | Decimal (inch to mm) |
| 1/64 | 0.015625 | 0.396875 | |||||
| 2/64 | 1/32 | 1/16 | 0.03125 | 0.79375 | |||
| 3/64 | 0.046875 | 1.190625 | |||||
| 4/64 | 2/32 | 0.0625 | 1.5875 | ||||
| 5/64 | 0.078125 | 1.984375 | |||||
| 6/64 | 3/32 | 0.09375 | 2.38125 | ||||
| 7/64 | 0.109375 | 2.778125 | |||||
| 8/64 | 4/32 | 2/16 | 1/8 | 0.125 | 3.175 | ||
| 9/64 | 0.140625 | 3.571875 | |||||
| 10/64 | 5/32 | 0.15625 | 3.96875 | ||||
| 11/64 | 0.171875 | 4.365625 | |||||
| 12/64 | 6/32x | 3/16 | 0.1875 | 4.7625 | |||
| 13/64 | 0.203125 | 5.159375 | |||||
| 14/64 | 7/32 | 0.21875 | 5.55625 | ||||
| 15/64 | 0.234375 | 5.953125 | |||||
| 16/64 | 8/32 | 4/16 | 2/8 | 1/4 | 1/4 | 0.25 | 6.35 |
| 17/64 | 0.265625 | 6.746875 | |||||
| 18/64 | 9/32 | 0.28125 | 7.14375 | ||||
| 19/64 | 0.296875 | 7.540625 | |||||
| 20/64 | 10/32 | 5/16 | 0.3125 | 7.9375 | |||
| 21/64 | 0.328125 | 8.334375 | |||||
| 22/64 | 11/32 | 0.34375 | 8.73125 | ||||
| 23/64 | 0.359375 | 9.128125 | |||||
| 24/64 | 12/32 | 6/16 | 3/8 | 0.325 | 9.525 | ||
| 25/64 | 0.390625 | 9.921875 | |||||
| 26/64 | 13/32 | 0.40625 | 10.31875 | ||||
| 27/64 | 0.421875 | 10.715625 | |||||
| 28/64 | 14/32 | 7/16 | 0.4375 | 11.1125 | |||
| 29/64 | 0.453125 | 11.509375 | |||||
| 30/64 | 15/32 | 0.46875 | 11.90625 | ||||
| 31/64 | 0.484375 | 12.303125 | |||||
| 32/64 | 16/32 | 8/16 | 4/8 | 2/4 | 2/4 | 0.5 | 12.7 |
| 33/64 | 0.515625 | 13.096875 | |||||
| 34/64 | 17/32 | 0.53125 | 13.49375 | ||||
| 35/64 | 0.546875 | 13.890625 | |||||
| 36/64 | 18/32 | 9/16 | 0.5625 | 14.2875 | |||
| 37/64 | 0.578125 | 14.684375 | |||||
| 38/64 | 9/32 | 0.59375 | 15.08125 | ||||
| 39/64 | 0.609375 | 15.478125 | |||||
| 40/64 | 20/32 | 10/16 | 5/8 | 0.625 | 15.875 | ||
| 41/64 | 0.640625 | 16.271875 | |||||
| 42/64 | 21/32 | 0.65625 | 16.66875 | ||||
| 43/64 | 0.671875 | 17.065625 | |||||
| 44/64 | 22/32 | 11/16 | 0.6875 | 17.4625 | |||
| 45/64 | 0.703125 | 17.859375 | |||||
| 46/64 | 23/32 | 0.71875 | 18.25625 | ||||
| 47/64 | 0.734375 | 18.653125 | |||||
| 48/64 | 24/32 | 12/16 | 6/8 | 3/6 | 3/6 | 0.75 | 19.05 |
| 49/64 | 0.765625 | 19.446875 | |||||
| 50/64 | 25/32 | 0.78125 | 19.84375 | ||||
| 51/64 | 0.796875 | 20.240625 | |||||
| 52/64 | 26/32 | 13/16 | 0.8125 | 20.6375 | |||
| 53/64 | 0.828125 | 21.034375 | |||||
| 54/64 | 27/32 | 0.84375 | 21.43125 | ||||
| 55/64 | 0.859375 | 21.828125 | |||||
| 56/64 | 28/32 | 14/16 | 7/8 | 0.875 | 22.225 | ||
| 57/64 | 0.890625 | 22.621875 | |||||
| 58/64 | 29/32 | 0.90625 | 23.01875 | ||||
| 59/64 | 0.921875 | 23.415625 | |||||
| 60/64 | 30/32 | 15/16 | 0.9375 | 23.8125 | |||
| 61/64 | 0.953125 | 24.209375 | |||||
| 62/64 | 31/32 | 0.96875 | 24.60625 | ||||
| 63/64 | 0.984375 | 25.003125 | |||||
| 64/64 | 32/32 | 16/16 | 8/8 | 4/4 | 2/2 | 1 | 25.4 |
Explore our Popular Online Course
| MBA Online | BCA Online |
| MCA Online | B.Com Online |
| M.Com Online | BBA Online |
| M.Sc Online | B.Sc Online |
| One Year MBA Online | Click Here For More Online Programs |
A Quick Insight of College Vidya
The online education market in India remains disorganised, making it difficult for students to find relevant resources. We are the first online platform in India to consolidate all of the available online learning universities into a single location.
College Vidya equips students with the tools they need to enrol in top online universities. Our compare tool allows you to quickly and easily evaluate different online colleges based on a variety of criteria, including tuition, e-learning system, EMI, faculty, and more
FAQs on The Fraction Calculator
Calculating fractions is very easy: for addition and subtraction convert the fractions to a like pair and then perform the necessary operations. For multiplication or division you can directly perform the calculations on the fractions.
3/4 divided by 2 will be equal to 3/8.
The ½ of ¾ is ⅜.
¼ x ¼ as a fraction will be ⅛
You can divide fractions by first inverting the divisor fraction and multiplying the dividend fraction by it. The answer should be reduced to the simplest form. For example:

To compare fractions, convert them into like fractions first. After that, compare the numerators of the like fractions and the one with the greater numerator is larger. Unlike fractions cannot be compared directly.
To add fractions with different denominators, firstly convert the fractions to like fractions to obtain the same denominator (which will be the LCM of the two denominators). After this, add the numerators and then reduce the obtained answer to the simplest form.
A mixed fraction is a fraction figure that has two parts: a whole number and a fraction.
No, mixed fractions can only be obtained from improper fractions since their denominators are smaller than the numerators, which means upon long division, a positive remainder will be obtained. On the other hand, for proper fractions, the long division will either not give a remainder (the dividend being smaller than the divisor) or give a zero remainder. So proper fractions cannot form mixed fractions.
To add/subtract two mixed fractions, convert them into improper fractions first and then perform the operations like other fractions.
Get Free Consultation
All Calculators
- Age Calculator
- Education Loan EMI Calculator
- Percentage Calculator
- BMI Calculator
- INR to USD Converter
- Return on Investment (ROI) Calculator
- Fraction Calculator
- Gallon To Liter Calculator
- Meter & Feet Calculator
- SGPA To Percentage Calculator
- CGPA To Percentage Calculator
- GPA To Percentage Calculator
- Inch To Centimeter Calculator
- Cat Percentile Calculator
- acre to square feet calculator
- acres to square meters calculator
- billion to rupees calculator
- binary to hex calculator
- centimeters to millimeters calculator
- centimeter to feet calculator
- centimeter to meter calculator
- cubic foot to cubic meter calculator
- decameters to meters calculator
- decimal to fraction calculator
- feet to centimeters calculator
- hectare to acre calculator
- hours to minutes calculator
- inches to feet calculator
- kilometer to miles calculator
- lbs to kg calculator
- meter to inch calculator
- meter to kilometer calculator
- meter to millimeter calculator
- meters to centimeters calculator
- militmeter to inches calculator
- millimeters to centimeters calculator
- million to crore calculator
- million to lakhs calculator
- million to rupees calculator
- square foot to square meter calculator
- square meter to square feet calculator
- volume of cuboid calculator